On Temporal Evolution of Information-Theoretic Descriptors of Molecular Electronic Structure
Roman F Nalewajski
DOI10.21767/2470-9905.100030
Roman F Nalewajski*
Department of Theoretical Chemistry,Jagiellonian University, Gronostajowa 2, 30-387 Cracow, Poland
*Corresponding Author:
Roman F Nalewajski
Department of Theoretical Chemistry
Jagiellonian University, Gronostajowa 2
30-387 Cracow, Poland
Tel: +48725020075
Fax: +48126632024
E-mail: nalewajs@chemia.uj.edu.pl
Received date: December 20, 2017; Accepted date: January 01, 2018; Published date: January 08, 2018
Citation: Nalewajski RF (2018) On Temporal Evolution of Information-Theoretic Descriptors of Molecular Electronic Structure. Struct Chem Crystallogr Commun Vol.4 No.1:1. doi:10.21767/2470-9905.100030
Abstract
The dynamics of probability (modulus) and phase (current) components of general electronic states is used to determine the temporal evolution of the overall descriptors of the information (determinicity) and entropy (indeterminicity) content of complex molecular states. These resultant information-theoretic concepts combine the classical (probability) contributions of Fisher and Shannon, and the corresponding nonclassical supplements due to the state phase/current. The total time derivatives of such overall measures of the gradient information and complex entropy are determined from Schrödinger’s equation using the chainrule transformations. These overall productions of the gradient information and complex entropy are shown to be of a purely nonclassical origin, thus identically vanishing in real electronic states, e.g., the nondegenerate ground state of a molecule.
Keywords
Fisher information; Information continuity/dynamics; Non classical information/entropy; Quantum information theory; Shannon entropy
Introduction
The electronic structure of molecules is reflected by both the system electron density and its current distribution. One recalls that the continuity relation for the state probability density, which relates these two structural aspects, implies that the density dynamics is determined by current’s divergence. Therefore, to paraphrase Prigogine [1], while the particle density determines a static structure of “being”, the probability current delineates a dynamic structure of “becoming”. These two structural facets generate the associated classical and non-classical contributions to the resultant measure of the information/entropy content of the system complex electronic state [2]. A general electronic wave function is a complex entity characterized by its modulus and phase components. The square of the former defines the particle probability distribution, the structure of “being”, while the gradient of the latter generates the state current density, the structure of “becoming”.
The following tensor notation is adopted: A denotes a scalar, A is the row/column vector, A represents a square or rectangular matrix and the dashed symbol  stands for the quantummechanical operator of the physical property A. The logarithm of the Shannon information measure is taken to an arbitrary but fixed base: log=log2 corresponds to the information content measured in bits (binary digits), while log=ln expresses the amount of information in nats (natural units): 1 nat=1.44 bits.
stands for the quantummechanical operator of the physical property A. The logarithm of the Shannon information measure is taken to an arbitrary but fixed base: log=log2 corresponds to the information content measured in bits (binary digits), while log=ln expresses the amount of information in nats (natural units): 1 nat=1.44 bits.
The classical Information Theory (IT) [3-10], an important branch of the applied probability theory, has already provided with new insights into the molecular electronic structure and generated useful descriptors of atoms in molecules, reactivity preferences and patterns of chemical bonds, e.g., [11-15]. The familiar information/entropy measures of Fisher [3,4] and Shannon [5,6] only reflect the state information/entropy content due to the probability distribution, thus failing to distinguish states exhibiting the same electron density but different current compositions. The recently introduced resultant IT descriptors [2,16-22] combine these classical contributions with their respective nonclassical supplements due to the state phase/current. The densities of the nonclassical information/entropy terms exhibit the same mutual relations as their classical analogs and they introduce the nonvanishing source terms into their respective continuity relations [2]. They have been successfully used to establish the phase and information equilibria in molecules, and to distinguish the mutually bonded (phase-related, “entangled”) and non-bonded (phase-unrelated, “disentangled”) status of molecular fragments or reactants [23-28].
In the quantum IT description of equilibria in molecular systems and their constituent fragments one has to employ both the probability and phase/current aspects of their quantum states, in order to fully characterize the overall information content in molecular wave functions, the equilibrium states of both the system as a whole and its constituent parts, a degree of the quantum entanglement (mutual bonding status) of subsystems, or the electron diffusion processes [24]. In this analysis, after a brief summary of these novel IT concepts, we examine their temporal evolution using the probability and phase dynamics determined by the Schrödinger equation. The time dependence of the resultant information/entropy will be expressed in terms of the probability and phase degrees-of-freedom of molecular states. The total time derivatives of the average resultant gradient information and complex global entropy, integrals of the “source” terms in the associated continuity equations [2,24,26], will be derived via the spatial chain-rule transformations in terms of the relevant partial functional derivatives. They will be also interpreted within Schrödinger’s dynamical picture of quantum mechanics and their nonclassical origins will be revealed.
Probability and Phase/Current Components of Electronic States
For simplicity, let us consider a single electron (N=1) at time t0=0 in state  described by the associated wave function in position-representation,
described by the associated wave function in position-representation,
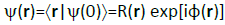 , (1)
, (1)
Where R(r) and φ(r) stand for its modulus and phase parts. Here, the complete basis 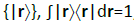 , combines the eigenvectors of the spatial position operator
, combines the eigenvectors of the spatial position operator  , i.e., the statevectors corresponding to the precise particle localizations {r}, the representation elementary events for the given time t0. At this very instant one determines the probability density, the expectation value of a local projection operator.
, i.e., the statevectors corresponding to the precise particle localizations {r}, the representation elementary events for the given time t0. At this very instant one determines the probability density, the expectation value of a local projection operator.
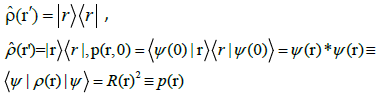 (2)
(2)
And its current density
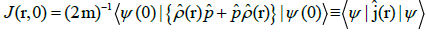 , (3)
, (3)
Where the particle momentum operator  is defined by its action on the wave function
is defined by its action on the wave function 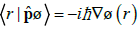 ,
,
 (4)
(4)
The local current is seen to combine the position probability density p(r) and the particle momentum per unit mass, i.e., the average velocity V(r)=p/m of the probability fluid, reflecting the state phase-gradient and measuring the average probabilitycurrent per particle:
V(r)=j(r)/p(r)=(ħ/m)∇φ(r). (5)
To summarize, the wave function modulus, the classical amplitude of the particle probability density, and the state phase or its gradient determining the effective velocity of the probability flux constitute two fundamental degrees-of-freedom in the full quantum IT treatment of electronic states in this illustrative one-electron system:  . The probability and phase “fluids” are fixed by the given electronic state. Since these parameters of the specified molecular wave function are neither “destroyed” nor “created” the source terms in their respective continuity equations must identically vanish.
. The probability and phase “fluids” are fixed by the given electronic state. Since these parameters of the specified molecular wave function are neither “destroyed” nor “created” the source terms in their respective continuity equations must identically vanish.
One envisages a single electron moving in the external potential due to the “frozen” nuclei of the molecule,
 (6)
(6)
described by the electronic Hamiltonian operator
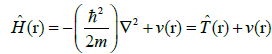 (7)
(7)
Where  denotes its kinetic part. The quantum dynamics of a general electronic state,
denotes its kinetic part. The quantum dynamics of a general electronic state,
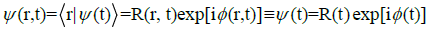 , (8)
, (8)
is determined by the Schrödinger equation (SE),
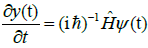 (9)
(9)
Which also determines temporal evolutions of the instantaneous probability density p(r, t)=|ψ(r, t)|2 = R(r, t)2 ≡ p(t) and of the state phase φ(r, t)≡φ(t). The time-derivative of the former expresses the source less continuity relation for the probability distribution,
 (10)
(10)
Interpreting the probability-source of the total derivative dp/dt as the time rate of change of the density in an infinitesimal volume element of the probability fluid as it moves in space, with the partial derivative ∂p/∂t similarly representing the corresponding rate at the fixed point in space,
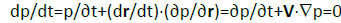 , (11)
, (11)
Identifies the last, convection term related to the effective velocity of Equation 5,
V⋅∇p=∇⋅j=V⋅∇p+p∇⋅V,(12)
and hence the vanishing “reaction” contribution [22] in this probability-balance equation:
p∇⋅V=0 or ∇⋅V= 0 .(13)
Therefore, the velocity field V(r) of the probability fluid is also source less in character.
Let us similarly examine the phase-field φ(r, t), fixed by the molecular state of Equation 8, and its conjugate current J(r, t)=φ(r, t) V(r, t). The phase-dynamics, derived from SE, reads:
∂φ/∂t=[ħ/(2m)] [R−1ΔR-(∇φ)2]-v/ħ
≡ − ∇⋅J=-V⋅∇φ or (14)
σφ ≡dφ/dt=∂φ/∂t+∇⋅J
=∂φ/∂t+(dr/dt).(∂φ/∂r)=∂φ/∂t+V⋅∇φ=0, (15)
A reference to Equation 14 shows that the time evolution of the state phase is shaped by the spatial inhomogeneity of this component, reflected by∇φ, and the effective velocity V of the probability-flux.
Next, let us examine some “geometrical” implications of the continuity relations for the state probability distribution (Equation 10 and 11) and its phase (Equation 14 and 15). When combined with the effective particle velocity of Equation 5 the former predicts
∇⋅ j=V⋅∇p=(ħ/m) ∇φ ⋅∇p,(16)
While the latter gives
∇⋅ J=V⋅∇φ=(ħ/m) (∇φ)2 (17)
It thus follows from Equation 16 that gradients of the probability and phase state parameters determine a locally perpendicular fields: ∇φ(r)⋅∇p(r)=0. The preceding equation similarly implies the following expression for the squared phase-gradient:
(∇φ)2=(2m/ħ2) v-R−1ΔR=(2m/ħ2) v-½ Δlnp. (18)
Classical and Nonclassical Information Descriptors
The (position, time) arguments of both components of general wave functions and the distributions they determine, both scalar or vector in character, e.g., R(r, t), p(r, t), φ(r, t), or j(r, t), V(r, t), J(r, t), define elementary events in the full informationtheoretic description of the molecular electronic structure. The nonvanishing phase/current field determines the dynamics of the probability distribution. The probability gradients reflects the spatial inhomogeneity of the electron distribution, while the dynamical derivative ∂p/∂t, related to the divergence (spatial inhomogeneity) of the probability current, supplements ∇p with the missing temporal component. Therefore, the combined (space, time) “gradients” (∂p/∂r, ∂p/∂t =-∇⋅j) together provide the complete structural characteristics of the given electronic state. Therefore an adequate (resultant) measure of the state information content should combine contributions due to all the gradient components.
One observes that the classical measures of the Fisher gradient information [3,4],
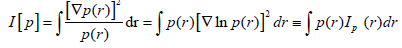 (19)
(19)
and Shannon’s [5,6] global entropy,
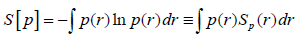 (20)
(20)
Focus exclusively on the “static” structural element, reflected by spatial variations of the probability density at specified time t0: p(r, t0)=p(r). The average information for locality events then explores only the spatial inhomogeneity of the probability distribution, reflected by its position-gradient. The densitiesper- electron of these two classical measures are seen to be mutually related, with the squared gradient of entropy density determining its Fisher analog:
Ip(r)=[∇Sp(r)]2. (21)
The classical descriptors I[p] and S[p] of the entropy/information content provide adequate measures for the nondegenerate stationary states corresponding to the sharply specified energies {En ≤ En+1}, Eigen functions of the electronic Hamiltonian of Equation (7),

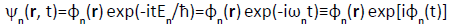 . (22)
. (22)
These states exhibit the vanishing spatial-phase, φn(r)=0, in the overall phase component φ(r, t)=φ(r)+φ(t), and hence φn(r)=Rn(r) and the vanishing current jn(r)=0. They give rise to the timeindependent probability density pn(r)=Rn(r)2 and stationary conditional probabilities of observing {|ψn} in a general state
 .
.
These classical average measures naturally generalize into their resultant descriptors combining the probability and phase/ current contributions to the overall entropy/information content in the quantum electronic state ψ [2,11-22] These generalized concepts are applicable to complex wave functions of molecular quantum mechanics. They are defined as expectation values of the associated operators: the Hermitian operator of the gradient information [29]  , related to the kinetic energy operator
, related to the kinetic energy operator  and the non-Hermitian entropy operator [30]
and the non-Hermitian entropy operator [30] 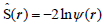 :
:
 (23)
(23)
 (24)
(24)
For general complex state of Equations 1 and 8 one identifies the classical (real) components of Equation 16 and 17, due to the state modulus/probability distribution, and supplementing nonclassical contributions, due to the state phase/current:
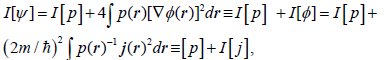 (25)
(25)
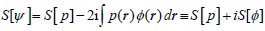 . (26)
. (26)
Their resultant densities-per-electron [see Equation (23) and (24)],
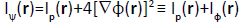 and
and
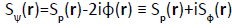 , (27)
, (27)
Now satisfy the complex-generalized relation [compare Equation (18)]:
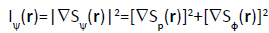 . (28)
. (28)
One observes that Equation (18) gives the alternative expression for the state resultant density of the gradient information:
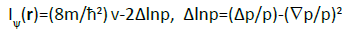 (29)
(29)
To summarize, the modulus (probability) and phase (current) components of electronic states generate the spatial and temporal elements of the molecular electronic structure. They are both accounted for in the resultant measures of the gradient or global descriptors of the information/entropy content in complex wave functions of molecular quantum mechanics. These generalized descriptors combine the familiar classical functional of the system probability density and their nonclassical supplements due to the current density. Their densities satisfy classical relations linking the gradient and global information/ entropy descriptors, appropriately generalized to cover the complex electronic states.
Temporal evolution of resultant information descriptors
It is of interest to examine the dynamics of resultant measures of the entropy/information content in the quantum state ψ(t):
I[ψ(t)]=I[p(t)]+I[φ(t)]=I[p(t)]+I[j(t)]≡I(t) and
S[ψ(t)]=S[p(t)]+iS[φ(t)]≡S(t). (30)
One can determine their temporal derivatives directly, using the relevant chain-rule transformations over all admissible (fixed) locations in space and the probability/phase continuities expressed by divergencies of Equations.16 and 17. For example, the time derivative of the classical Fisher information I[p] gives
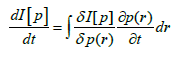 (31)
(31)
Where:
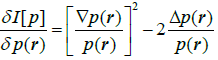 and
and
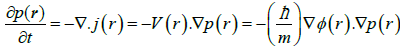 . (32)
. (32)
For the non-classical gradient information I [φ] one similarly finds:
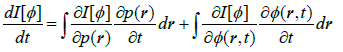 (33)
(33)
With the underlying partial derivatives:
 and
and
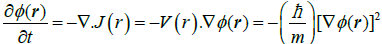 . (34)
. (34)
Combined contributions of Equation 31 and 33 finally determine the time derivative of the resultant gradient information:
σI(t)≡dI(t)/dt=dI[p]/dt+dI[]/dt
 (35)
(35)
One observes that this net change of the resultant gradient information vanishes in the real electronic state, when φ(r)=0, e.g., in the nondegenerate ground state.
The chain-rule generating the time derivative of the classical (Shannon) global entropy reads
 (36)
(36)
While that for transforming its nonclassical companion gives:
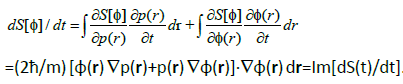 (37)
(37)
These two contributions generate the following resultant derivative of the complex entropy of Equation 26:
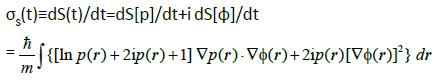 (38)
(38)
Again, this total temporal derivative of the complex entropy is seen to be of entirely nonclassical origin, vanishing identically for the zero phase-gradient (current).
Discussion
Let us reexamine this temporal evolution of the overall information/entropy descriptors using Schrödinger’s dynamical “picture” of molecular quantum mechanics. In this framework the time change of the resultant gradient information, the operator of which does not depend on time explicitly,
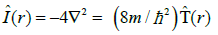 (39)
(39)
Results solely from a dependence of the system state vector 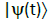 itself:
itself:
 (40)
(40)
One recalls that 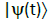 is generated by the action of the (unitary) time-evolution operator
is generated by the action of the (unitary) time-evolution operator  ,
,
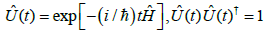 (41)
(41)
On the initial state 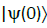 :
:
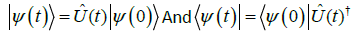 (42)
(42)
It then follows from SE 9 that the time derivative of the resultant Fisher-type descriptor, of the gradient (determinicity) information, is generated by the expectation value of the commutator 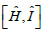 :
:
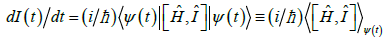 (43)
(43)
The familiar commutator identities give
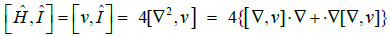 (44)
(44)
Where [∇, v]=∇v, and the integration by parts,
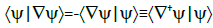 , (45)
, (45)
Implies ∇†=-∇. Hence the derivative of Equation 43 reads:
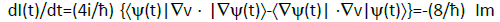
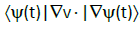 . (46)
. (46)
Using Equation 5 and 8 finally gives:
σI(t)≡dI(t)/dt =-(8m/ħ2) ∫R(r, t) ∇v(r) .V(r) dr (47)
This total derivative of the resultant gradient information is thus determined by the current content of the molecular electronic state, reflected by the effective velocity field V(r), with the product of probability amplitude and gradient of the external potential providing a local weighting factor. It identically vanishes for the zero current density everywhere. One thus confirms its nonclassical origin (compare Equation. 35).
Turning now to the resultant complex entropy of Equations 24 and 26,
 (48)
(48)
One observes that its (non-Hermitian) operator,
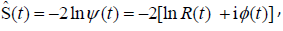 (49)
(49)
is explicitly time dependent. This modifies the expression for the time derivative of this complex measure of the overall state uncertainty by the extra term:
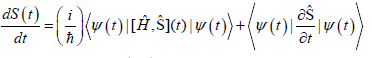 (50)
(50)

This Hellmann-Feynman−type contribution represents the expectation value in state ψ(t) of the operator derivative
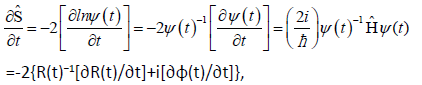 (51)
(51)
Where R−1(∂R/∂t)=½ ∂lnp/∂t (see also Equation 10) and the phase dynamics is determined in Equation 14. Its physical meaning is revealed by SE, which has been used in the preceding equation,
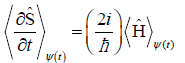 (52)
(52)
Therefore, this purely imaginary contribution is proportional to the state average energy  .
.
In determining the commutator term in Equation 50 one again uses the following identities:
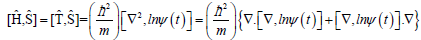 (53)
(53)
Where the elementary entropy commutator (see Equation 8)
[∇, lnψ(t)]=∇lnψ(t)=∇lnR(t)+i∇φ(t)=R(t)−1∇R(t)+i∇φ(t)=½∇lnp(t) +i∇φ(t) (54)
This contribution to the time derivative of the average complex entropy thus reads:
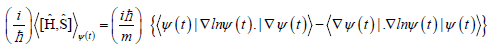
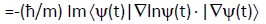 (55)
(55)
Therefore, this term determines the real part of the complex derivative of Equation 50, while Equation 52 generates its imaginary part:
dS(t)/dt=(dS[p]/dt)+i (dS[φ]/dt)=Re[dS(t)/dt]+i Im[dS(t)/dt],
 (56)
(56)
It should be finally remarked that the time derivative of the average information in state ψ(t) (Equation 23), I(t)=dI(t)/dt, can be also expressed as the spatial integral over its density σI(r)=dI(r)/ dt representing the local source (production) term in the information continuity equation [2,25]. It assumes the classical form [26,31], as the sum over the state independent probability and phase components k ∈ (p, φ) of the corresponding products of the information affinities (“perturbations”) {Gk(r)=∇Fk(r)}, gradients of the associated intensities {Fk(r)} defined by the partial functional derivatives
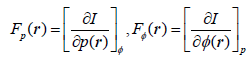 (57)
(57)
and the conjugate fluxes (“responses”) {Jk(r)}∈{j(r), J(r)}:
σI(r)=Σk Gk(r) . Jk(r) (58)
Conclusion
The need for the nonclassical (phase/current) supplements of the classical (probability) measures of the information content in molecular states has been stressed. The electron density distribution determines a static facet of the molecular structure, while the current distribution describes its dynamic aspect. Both these structural manifestations contribute to the overall information content of a generally complex electronic state of molecular systems, reflected by the resultant IT concepts. The total time derivatives of such entropic descriptors of electronic structure have been examined. These time dependencies have been established via the Schrödinger equation and the dynamics/continuity of the classical and nonclassical degrees-offreedom of complex wave functions it implies. The nonclassical origins of the net temporal changes in the overall entropy/ information quantities have been demonstrated. Therefore, for the nondegenerate electronic states, which exhibit the vanishing local phase and current components, the time derivatives of the resultant gradient information and global entropy exactly vanish.
Although, for simplicity reasons, we have assumed one-electron case, the modulus (density) and the phase (current) aspects of general electronic states can be similarly separated using the Harriman-Zumbach-Maschke (HZM) construction [32,33] in the Density Functional Theory (DFT) [34-36], of the Slater determinants yielding the specified electron density. The present single electron development can be then naturally generalized into many-electron states of atomic and molecular systems [2].
References
- Prigogine I (1980) From being to becoming: time and complexity in the physical sciences. Freeman WH & Co, New York, USA.
- Nalewajski RF (2016) Quantum information theory of molecular states. Nova Science Publishers, New York, USA.
- Fisher RA (1925) Proc Cambridge Phil Soc 22: 700.
- Frieden BR (2004) Physics from the Fisher information-a unification. 2nd edn. Cambridge University Press, Cambridge, UK.
- Shannon CE (1948) Bell System Tech J 27: 379, 623.
- Shannon CE, Weaver W (1949) The mathematical theory of communication. University of Illinois, Urbana.
- Kullback S, Leibler RA (1951) On Information and Sufficiency in Ann. Math Stat 22: 79-86.
- Kullback S (1959) Information theory and statistics. Wiley, New York, USA.
- Abramson N (1963) Information theory and coding. McGraw Hill, New York, USA.
- Pfeifer PE (1978) Concepts of probability theory. 2nd edn. Dover, New York, USA.
- Nalewajski RF (2006) Information theory of molecular systems. Elsevier, Amsterdam.
- Nalewajski RF (2010) Information origins of the chemical bond. Nova Science Publishers, New York, USA.
- Nalewajski RF (2012) Perspectives in electronic structure theory. Springer, Heidelberg, pp: 91-92.
- Nalewajski RF, Parr RG (2000) Information theory, atoms in molecules and molecular similarity. Proc Natl Acad Sci USA 97: 8879-8882.
- Parr RG, Ayers PW, Nalewajski RF (2005) The Journal of Physical Chemistry A. J Phys Chem A 109: 3957-3959.
- Nalewajski RF (2013) Electronic communications and physical bonds. Ann Phys (Leipzig) 525: 256, 351.
- Nalewajski RF (2014) On phase-equilibria in molecules. J Math Chem 52: 588-612.
- Nalewajski RF (2014) On phase-equilibria in molecules. J Math Chem 52: 1921-1948.
- Nalewajski RF (2014) On phase/current components of entropy/information descriptors of molecular states. Mol Phys 112: 2587-2601.
- Nalewajski RF (2016) On phase/current components of entropy/information descriptors of molecular states. Mol Phys 114: 1225.
- Nalewajski RF (2015) Phase/current information descriptors and equilibrium states in molecules. Int J Quantum Chem 115: 1274-1288.
- Nalewajski RF (2015) Advances in mathematics research. Volume 19. Nova Science Publishers, New York, USA, p: 53.
- Primas H (1981) Chemistry, quantum mechanics and reductionism. Springer-Verlag, Berlin.
- Nalewajski RF (2015) Advances in mathematics research. Volume 22. Nova Science Publishers, New York, USA.
- Nalewajski RF (2016) Trends Phys Chem 16: 71.
- Nalewajski RF (2016) Trends Phys Chem (In Press).
- Nalewajski RF (2017) Conceptual density functional theory. Apple Academic Press, Waretown (In Press).
- Nalewajski RF (2017) Chemical Reactivity Description in Density-Functional and Information Theories. Acta Physico-Chimica Sinica 33: 2491-2509.
- Nalewajski RF (2008) Int J Quantum Chem 108: 2230.
- Nalewajski RF (2016) Complex entropy and resultant information measures. J Math Chem 54: 1777-1782.
- Callen HB (1960) Thermodynamics: An introduction to the physical theories of equilibrium thermostatics and irreversible thermodynamics. Wiley, New York, USA.
- Harriman JE (1981) Orthonormal orbitals for the representation of an arbitrary density. Phys Rev A 24: 680.
- Zumbach G, Maschke K (1983) Erratum: New approach to the calculation of density functionals. Phys Rev A 28: 544; Erratum (1984) Phys Rev A 29: 1585.
- Hohenberg P, Kohn W (1964) Inhomogeneous Electron Gas. Phys Rev 136: B864.
- Kohn W, Sham LJ (1965) Self-Consistent Equations Including Exchange and Correlation Effects. Phys Rev 140A: 1133.
- Levy M (1979) Universal variational functionals of electron densities, first-order density matrices, and natural spin-orbitals and solution of the v-representability problem. Proc Natl Acad Sci USA 76: 6062-6065.
Open Access Journals
- Aquaculture & Veterinary Science
- Chemistry & Chemical Sciences
- Clinical Sciences
- Engineering
- General Science
- Genetics & Molecular Biology
- Health Care & Nursing
- Immunology & Microbiology
- Materials Science
- Mathematics & Physics
- Medical Sciences
- Neurology & Psychiatry
- Oncology & Cancer Science
- Pharmaceutical Sciences
