Effectiveness of Imidazoline in Mitigating Transport Pipeline Corrosion
Michael K Akindeju, Emmanuel O Obanijesu, Matthew Edwards Rebecca Boyanich and Harvinder Mohar
DOI10.21767/2470-9905.100026
Michael K Akindeju*, Emmanuel O Obanijesu, Matthew Edwards Rebecca Boyanich and Harvinder Mohar
MKPro Engineering Private Limited, Ballarat Central, Victoria, Australia
- *Corresponding Author:
- Michael K Akindeju
Principal Consulting Process Engineer
MKPro Engineering Private Limited
Ballarat Central, Victoria
Australia
Email: michael.akindeju@mkproengineering.com
Tel: +61449205856
Received date: March 15, 2017; Accepted date: April 07, 2017; Published date: April 12, 2017
Citation: Akindeju MK, Obanijesu EO, Edwards M, et al. Effectiveness of Imidazoline in Mitigating Transport Pipeline Corrosion. Struct Chem Crystallogr Commun. 2017, 3:1.
Abstract
The detrimental effects of corrosion in transportation pipelines have been a primary issue for the oil and gas industry for many years. Every year, millions of dollars are invested into corrosion inhibitors in order to minimise corrosions implication on flow assurance. Imidazoline and its derivatives have been a prevalent corrosion inhibitor owing to its good adsorption characteristics and film forming capabilities; however, there remains some uncertainty in literature pertaining to the effect of temperature on its performance. GULP simulation software was used to study the effect of temperature on the thermodynamic properties of imidazoline in carbon steel pipelines. Entropy, heat capacity, Helmholtz free energy, entropy and Gibbs free energy were influenced by changes in temperature. An optimal operating range was found to exist between 298K and 333K. Within this range, spontaneous chemisorption was occurring and the imidazoline molecules possessed enough kinetic energy to displace any bound water on the metal surface to permit the preferential adsorption of the imidazoline head group. However, beyond 333K, the kinetic energy of the system hindered the steady formation of the protective barrier, reducing its inhibitive potential. This study agrees with previous literature on the effect of temperature on the ability of imidazoline as a corrosion inhibitor, however further studies into the effect of pipeline conditions and imidazoline molecular structure are needed in order to affirm the optimal applicability of imidazoline as a corrosion inhibitor.
Keywords
Gas transport; Pipeline; Corrosion; Imidazoline
Introduction
Oil and gas provides about 54% of global primary energy requirement. Its transportation from fields to final consumers profoundly relies on high pressure pipelines with current global total length given as over 3500000 km [1]. However, the detrimental impacts of corrosion in these pipelines have been a prevailing issue for the industry for many years. It heavily imposes threats on the industry through economic, environmental and safety issues. Injection of corrosion inhibitor into pipelines is presently the most economically feasible solution and immidazoline is a major corrosion inhibitor used in the subsea pipelines to minimize sweet corrosion.
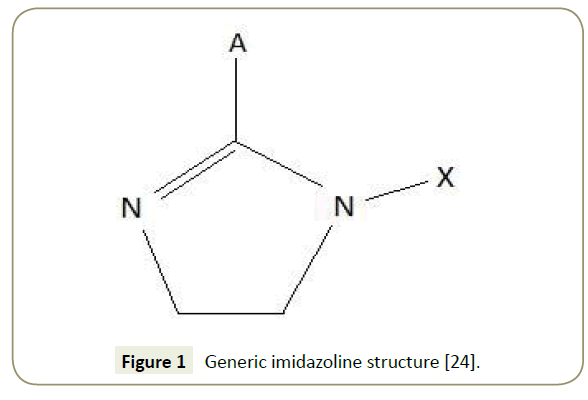
Imidazoline and its derivatives are extensively used due to its to their good adsorption characteristics and film forming capabilities [2] and high activity rates in acidic mediums [3]. Synthesis of imidazoline molecules is achieved by a simple process using relatively cheap materials. The general molecular structure of imidazoline is presented in Figure 1.
Imidazoline molecules inhibit corrosion by providing a thin film physical interface between the piping material and the fluid in transport along the pipe wall [4]. Adsorption to the metal surface occurs at the ring and at times, the pendant chain, due to the high dipole value between the metal surface and the imidazoline [5], leaving the alkyl chains to form a protective film [6]. As multiple adsorptions occur, a self-assembled mono-layer will form that has the potential to develop into a bilayer or multilayer given the right temperature, concentration and solubility conditions [7].
Interaction between the metal surface and imidazoline is established through physisorption or chemisorption. Physisorption involves the electrostatic interaction between the charged inhibitor molecules and the steel microstructure [8]. Permanent positive poles are created on the hydrogen and carbon atoms and negative poles on the nitrogen due to the inherent difference in electronegativity of atoms in the natural arrangement of the imidazoline molecule [9]. This polar arrangement forms the basis of the interaction with the ionic distribution of the steel microstructure [6]. While electrostatic forces create the movement of molecules to the wall, these forces, however, are not enough to retain the molecules in place.
Chemisorption, typically occurring after physisorption, involves charge sharing through coordinate covalent bonds (π bonds) resulting in much stronger adsorption [10]. Movement of valence electrons occurs between the Highest Occupied Molecular Orbital (HOMO) and the Lowest Unoccupied Molecular Orbital (LUMO) of the imidazoline and metal surface forming strong covalent [11]. LUMOs are concentrated on the hydrophilic ring. Consequently, reactive regions are not expected to be correlated to the long hydrocarbon straight chain [12]. Iron molecules in excited state house electrons in their d orbitals and these form a coordinate bond with the nitrogen atoms [12], further strengthening the chemisorption [9]. Conversely, unoccupied d orbitals in Fe accept electrons from the HOMO in the Imidazoline ring forming a coordinate covalent bond [7].
There are several factors effecting imidazoline as a corrosion inhibitor. These include the pedant chain structure, alkyl chain length and tilt, solubility, concentration, permeability, presence of impurities, natural gas velocity and operating temperature [11,13-16]. Tan et al. [13] provided an hypothesis that imidazoline compounds did not adhere to established adsorption models; this was however disproved by Mazumber et al. [11] using the Langmuir isotherm adsorption mechanism under certain conditions. It was identified by Cruz et al. [17] that the head group of imidazoline was essential to its adsorption due to the electron rich N=C-N region. The pendant chain structure also influences the adsorptive capabilities of imidazoline; however, the adsorption ability of the head group should not change as the pendant group is substituted [18]. The presence of lone pairs on the chain allows the formation of co-ordinate covalent bonds, thus improving adsorption [19]. Further, the attachment of a polar group to the pendant chain will increase the hydrophilic nature due to the polar nature of water [20]. Jovancicevic et al. [14] concluded that at a critical micelles concentration (CMC), imidazoline is highly dispersible. This suggests the imidazoline will be rapidly transported to the metal surface where they will form a stable boundary layer; however, concentrations higher than the CMC will be superfluous.
Many attempts have been made to establish the inhibition capacity of imidazoline in natural gas pipelines. Most of these studies however, only predict the adsorption due to factors such as concentration, pendant chain length and pendant chain structure [16,18,20]. Experimental work by Edwards et al. [16] conducted mechanistic studies through bubble and loop tests to qualitatively examine the adsorption, coverage, interaction strength and rate of adsorption to a metal surface between different imidazoline derivatives. Edwards findings illustrate the interdependence between molecular structures, concentration and flow patterns.
Further experimental work by Ramachandran et al. [20] established a linear relationship between the alkyl chain length and minimum effective concentration for chain lengths between 12 to 20 atoms.
The effect of different pendant chains for compounds with different hydrophilic head groups was studied by Zhung et al. [18] to evaluate the corrosion inhibition performance. Four undecyl-Imidazoline molecules were used, each with a different hydrophilic group attached; carboxymethyl, hydroxyethyl, aminoethyl and hydrogen. For the theoretical quantum chemistry calculations, the reactivity of the inhibitor molecules was determined by analysis of chemical potential, chemical hardness and electrophilicity index through the density functional theory. The relationships are given in Equations 1 to 3.
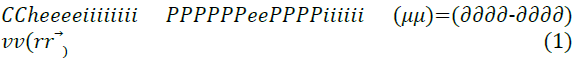
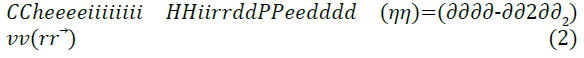
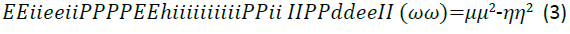
Zhung’s study analysed the interaction between the metal surface and their Self-Assembled Monolayer (SAM) for each of the Imidazoline molecule types, as well as the stability of this layer. These relationships are shown in Equations 4 and 5.
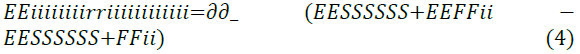
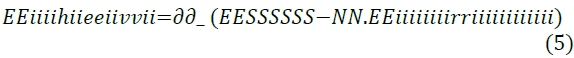
All of the tested Imidazoline molecules were capable of forming a self-assembled monolayer on the iron surface and calculations indicated that the atomic structure (ring bond angles and length) of the Imidazoline molecules do not deviate by a large extent when the pendant group is substituted. Highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) distribution changed with substitution of the pendant chain, which was crucial in the changing adsorption characteristics. Zhung’s work uses modelling methods to challenge previous speculative work of Edwards et al. [16] through focusing on the implications of swapping the pendant chain. The discussions and comparisons presented in the literature are also supported by reliable sources.
Despite the prevalent use of imidazoline as a corrosion inhibitor in the oil and gas industry there still remains a degree of uncertainty in literature regarding the impact temperature has on its effectiveness. This study investigated the effect of temperature on imidaoline performance by generating an Imidazoline molecule through the software GDIS (Graphical Display Interface for Structures) and exporting and running the simulations through GULP (General Utility Lattice Program) to minimize the energy of the system. Analysis of the mechanical properties and phonon will determine how the molecules behaviour will change with temperature.
Methodology
General Utility Lattice Program (GULP) was used to run the simulations to predict the trend of imidazoline adsorption with increasing temperature in carbon steel natural gas pipelines. GULP performs 3D energy minimization, crystal property and surface attachment energy calculations based on force field methods [21,22].
Simulation setup
Parameters used for the simulations such as lattice and intermolecular interaction energies obtained from literature were configured and run through GULP. Simulations were carried out at every 5K interval ranging from 298K to 398K and at 10K intervals thereafter until 498K to ensure a comprehensive dataset to identify any trends. The convergence accuracy was prescribed as 1 × 10-4 to yield a valid simulation.
Temperature dependant phonon including entropy, Helmholtz free-energy and heat capacity, thermodynamic properties including Gibbs free-energy, enthalpy and internal energy, as well as mechanical properties such as bulk modulus, shear modulus, s-wave velocity, p-wave velocity, compressibility and Young’s modulus were analysed in aid of interpreting the effect of temperature on the inhibitive effectiveness of imidazoline. A visual display of the simulated imidazoline molecule was subsequently produced using Graphical Display Interface for Structure (GDIS).
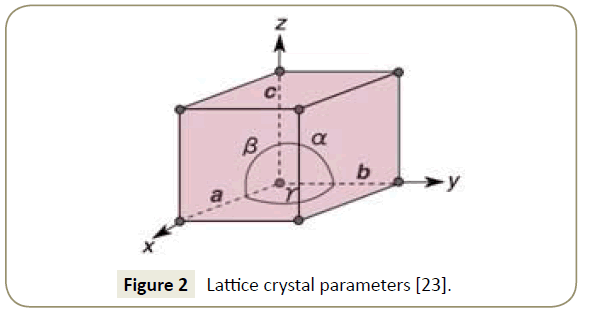
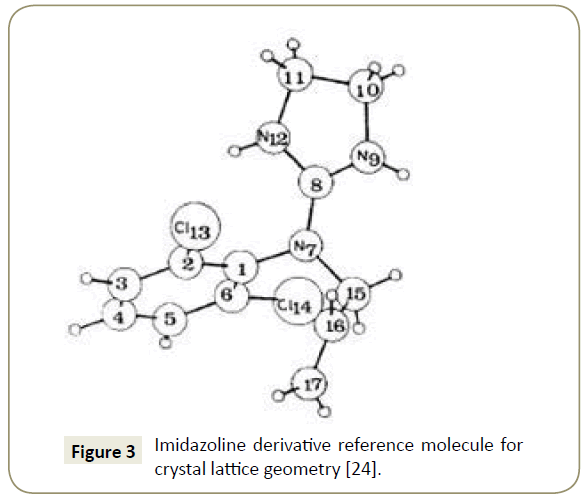
Imidazoline crystal lattice geometry: The geometry of a unit cell in three dimensions can be defined by the lattice geometry of a crystal structure using x, y and z crystallographic axis [23]. Determination of the origin of the coordinate system and the atomic position is achieved through the lattice points on the end of the axis. The general configuration showing the axes is presented in Figure 2. The lattice points used for this simulation were obtained from Carpy et al. [24] and are presented in Table 1. Figure 3 displays a reference molecule of an imidazoline derivative outlining the position of the atoms analysed in Table 1.
| x | y | z | BBBBBB/BB(AA2) | |
|---|---|---|---|---|
| C(1) | -1555(12) | -2402(8) | 2132(6) | 3.5(3) |
| C(2) | -3110(13) | -1721(10) | 2532(7) | 4.7(3) |
| C(3) | -4026(15) | -524(11) | 2120(8) | 6.3(4) |
| C(4) | -3502(18) | -99(12) | 1287(9) | 7.4(5) |
| C(5) | -2023(17) | -719(12) | 869(8) | 6.5(4) |
| C(6) | -1047(14) | -1900(11) | 1307(7) | 4.8(3) |
| N(7) | -629(10) | -3667(7) | 2536(5) | 3.9(2) |
| C(8) | 631(12) | -3314(9) | 3482(6) | 3.4(3) |
| N(9) | 1267(11) | -4404(8) | 4013(5) | 4.3(3) |
| C(10) | 2761(14) | -3601(10) | 4985(6) | 4.8(3) |
| C(11) | 2507(14) | -1841(10) | 5031(6) | 4.5(3) |
| N(12) | 1337(10) | -1817(7) | 3994(5) | 3.8(2) |
| Cl(13) | -3775(5) | -2838(4) | 3560(2) | 7.3(1) |
| Cl(14) | 891(5) | -2691(4) | 810(2) | 7.7(1) |
| C(15) | -1420(16) | -5362(10) | 1996(7) | 5.5(4) |
| C(16) | -3546(20) | -5855(12) | 1994(10) | 8.2(5) |
| C(17) | -5215(23) | -6082(15) | 1239(11) | 9.5(6) |
| Br(18) | 1914(2) | 1811(1) | 3358(1) | 5.0(0) |
| H(103) | -512(13) | -3(10) | 245(7) | 6.8 |
| H(104) | -414(14) | -77(11) | 97(7) | 7.7 |
| H(105) | -164(14) | -40(11) | 23(7) | 6.8 |
| H(109) | 125(14) | -535(11) | 380(7) | 6.7 |
| H(110) | 223(13) | -406(10) | 556(6) | 6.2 |
| H(210) | 422(13) | -374(10) | 496(6) | 5.6 |
| H(111) | 390(12) | -106(9) | 516(5) | 4.5 |
| H(211) | 175(12) | -146(10) | 556(6) | 5.6 |
| H(112) | 96(12) | -98(9) | 367(6) | 5.3 |
| H(115) | -134(13) | -545(10) | 127(6) | 6.3 |
| H(215) | -57(13) | -606(10) | 229(6) | 5.6 |
| H(116) | -372(16) | -596(13) | 269(8) | 9.0 |
| H(117) | -494(13) | -636(10) | 60(6) | 6.2 |
| H(217) | -663(13) | -598(11) | 134(6) | 7.3 |
Table 1: Crystal lattice points used for simulation (Carpy).
Imidazoline crystal lattice parameters: the length of the unit cell along the x, y and z axis are defined as vectors A, B and C respectively. Table 2 presents the vectors, is angstroms (Å), used in the simulation. Angles in the crystal lattice, referred to as α, β and γ, describe the angle between individual vectors [25]. α describes the angle between vectors b and c, β the angle between vectors a and c and γ the angle between vectors a and b. As can be seen in Table 2, angles of 90° were assumed for each of the angles for the purpose of the simulation.
| Vector | AA | Cell angles |
|---|---|---|
| A | 6.652 | 90ÃÆâÃâââ¬Å¾ÃâÃâ, α |
| B | 8.497 | 90ÃÆâÃâââ¬Å¾ÃâÃâ, β |
| C | 13.734 | 90ÃÆâÃâââ¬Å¾ÃâÃâ, γ |
Table 2: Lengths of crystal lattice parameter vectors (Carpy).
Buckingham potentials: The amount of energy in the chemical model is the main factor that affects molecular modelling [22]. The success of molecular modelling related to an energy state as close to zero as possible to ensure stability during the modelling process and to prevent the implosion of the model. Buckingham potentials are used in this molecular model for two-body short range interactions to ensure a zero-energy state [22]. The values of these potentials are influenced by the interatomic distance (r) between the imidazoline atoms. The Buckingham potentials for the respective imidazoline molecules in the simulation were calculated by Equation 6.
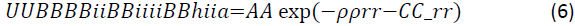
Buckingham potentials were taken from an input file used by Akindeju et all (ref) presented in Table 3. The obtained data is feasible and relevant to the molecular modelling of imidazoline as it measures the energy between the nitrogen, oxygen and carbon atoms. These atoms are the same atoms that are present in imidazoline molecules.
| Atom 1 | Atom 2 | Parameter 1 | Parameter 2 |
Parameter 3 |
Parameter 4 |
Parameter 5 |
|---|---|---|---|---|---|---|
| N | N | 4770.05261 | 0.2744725 | 15.177440 | 0.00 | 12.00 |
| N | C | 5420.51433 | 0.274725 | 19.513852 | 0.00 | 12.00 |
| N | H | 520.36938 | 0.271003 | 13.009234 | 0.00 | 12.00 |
| C | C | 3626.54091 | 0.277778 | 25.4113712 | 0.00 | 12.00 |
| C | H | 380.129829 | 0.27248 | 5.42051433 | 0.00 | 12.00 |
| H | H | 11508836 | 0.26738 | 1.18384033 | 0.00 | 12.00 |
Table 3: Buckingham potentials used in the simulation.
Molecular modelling
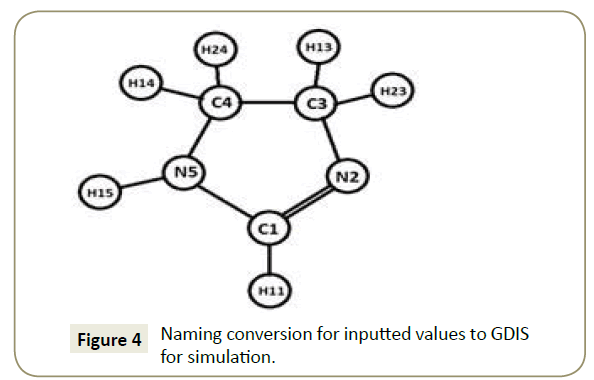
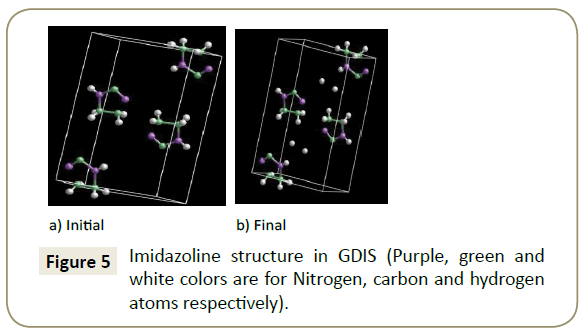
GDIS: The aforementioned parameters were adapted to a form that is recognizable to GDIS. Figure 4 shows the converted imidazoline molecule and (Table 4) the converted values in the x, y and z convention, which were then used to produce a model of the imidazoline in GDIS. The researched crystal parameters of imidazoline taken from Carpy et al. [24], have a nitrogen atom in place of the required hydrogen atom for the molecular modelling of an Imidazoline molecule. Due to this modification, the H11 atom did not adjoin to the C1 atom initially (refer to Figure 5a). This was rectified by manipulating the position of the H11 atom, however, the convergence threshold could not be attained; hence the final simulation was run without the H11 atom, Figure 5b.
| Atom | Reference | x | y | z |
|---|---|---|---|---|
| C1 | C8 | 0.0631 | 0.6686 | 0.3482 |
| H11 | N7 | 0.9371 | 0.6333 | 0.2536 |
| N2 | N9 | 0.1267 | 0.5596 | 0.4013 |
| C3 | C10 | 0.2761 | 0.6399 | 0.4986 |
| H13 | H110 | 0.223 | 0.594 | 0.556 |
| H23 | H210 | 0.422 | 0.626 | 0.496 |
| C4 | C11 | 0.2507 | 0.8159 | 0.5031 |
| H14 | H111 | 0.39 | 0.894 | 0.516 |
| H24 | H211 | 0.175 | 0.854 | 0.556 |
| N5 | N12 | 0.1337 | 0.8183 | 0.3994 |
| H15 | H112 | 0.096 | 0.902 | 0.367 |
Table 4: Imidazoline crystal parameter converted to format for GDIS input.
GULP: The projected imidazoline data was transferred to GULP simulation software. The facilitating and fitting of the Buckingham/interatomic potentials helps GULP in the energy minimization required for the stability of the molecular model of imidazoline. Based on literature, it has been identified that the effective system temperature for imidazoline spans from 290K to 350K and hence, rigorous simulations were run every 5K within this range whilst less rigorous simulations, of 10K increments, extend the scope of this study to 498K in order to confirm a basic trend. The molecular mechanics and energy minimization of the imidazoline model were studied at a constant pressure of 101.3 kPa for the respective temperatures in the range of 298K-423K.
Results and Discussion
Temperature dependant phonon
Simulation results showed that of the measured phonon, only Hemlholtz free energy, heat capacity and entropy varied with a change in temperature over the prescribed temperature range. The parameters which remained constant can be seen in Table 5.
| Atom | Reference | x | y | z |
|---|---|---|---|---|
| C1 | C8 | 0.0631 | 0.6686 | 0.3482 |
| H11 | N7 | 0.9371 | 0.6333 | 0.2536 |
| N2 | N9 | 0.1267 | 0.5596 | 0.4013 |
| C3 | C10 | 0.2761 | 0.6399 | 0.4986 |
| H13 | H110 | 0.223 | 0.594 | 0.556 |
| H23 | H210 | 0.422 | 0.626 | 0.496 |
| C4 | C11 | 0.2507 | 0.8159 | 0.5031 |
| H14 | H111 | 0.39 | 0.894 | 0.516 |
| H24 | H211 | 0.175 | 0.854 | 0.556 |
| N5 | N12 | 0.1337 | 0.8183 | 0.3994 |
| H15 | H112 | 0.096 | 0.902 | 0.367 |
Table 5: Constant Parameters in Simulation.
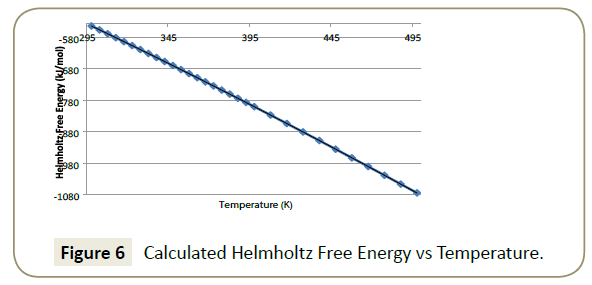
Helmholtz free energy: The results obtained for Helmholtz free energy are presented in Figure 6. It shows that Helmholtz free energy decreases with increasing temperature. The relationship between Helmholtz free energy and temperature is expressed by Equation 7 which shows a polynomial relationship to the second order.
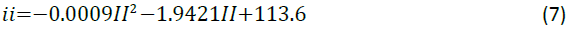
The correlation coefficient is obtained by Equation 8 and shows the degree to which the relationship correlated to the model. A value of 1 desirable as it correlates to a perfect model fit.
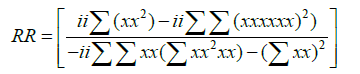 (8)
(8)
This simulation produced a perfect model fit with a correlation coefficient of 1. This means that results can be interpolated within the prescribed temperature range with a high degree of confidence.
Helmholtz free energy is defined by Equation 9 where A is the Helmholtz free energy (J), T is the temperature in (K) and S is the entropy (J/K).
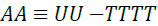 (9)
(9)
A measure of the negative difference in Helmholtz free energy dictates the maximum amount of extractable work from a system in which the temperature is held constant [26]. With a system at a constant volume, Helmholtz free energy must increase with an increase in temperature. As the maximum extractable work is the difference between the Helmholtz free energies at a particular temperature less a lower temperature, the result will be a positive value. This indicates that work is done by the system on the surroundings. As there is no volume change, the work is in the form of energy exchange with the pipe surface.
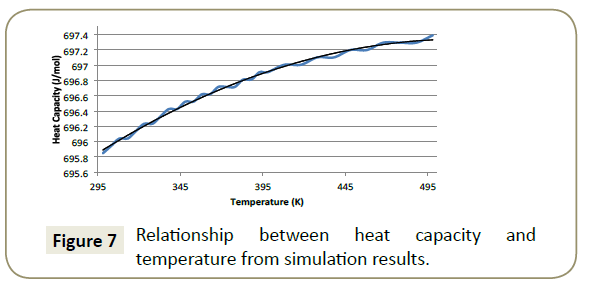
Heat capacity: Figure 7 presents the simulated results for the change in heat capacity with an increase in temperature. The of the imidazoline in GDIS. The researched crystal parameters of positive quadratic relationship is best described by Equation 10 with a correlation coefficient of 0.995.
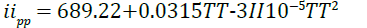 (10)
(10)
The quadratic nature is explained by Equations 11 and 12 as at constant pressure, the heat capacity is of the form;
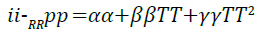 (11)
(11)
The results of the simulation, however, are conducted at constant volume rather than pressure.
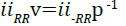 (12)
(12)
Applying Equation 12 at constant volume, the heat capacity constants for imidazoline pertaining to Equation
11 can be derived giving;
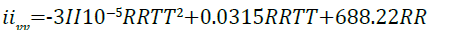 (13)
(13)
where R is the universal gas constant, R = 8.314 J/mol.K.
Heat capacity is the measure of ratio of heat added to a system to the resultant temperature change. Translational, rotational and vibrational (kinetic and potential) energy modes contribute to the heat capacity with the upper heat capacity limit attained when each of these modes are fully excited [26]. A greater value of heat capacity means that a smaller change in temperature is required to transfer a specific quantity of heat [26]. As the temperature of the system was increased, the heat capacity also increased meaning that a greater change in the systems temperature was caused by the addition of a specific quantity of heat. The maximum heat capacity was outside the scope of this modelling but approached approximately 697.7 J/mol.K. However, the higher the temperature, the less a specific quantity of heat added to the system changed the temperature, suggesting that up to a certain critical point, the energy required to raise the temperature is not worth the gain in heat capacity.
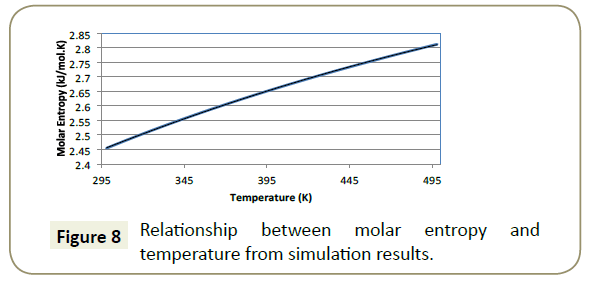
Entropy: The relationship between entropy with changing temperature from the simulation results are presented in Figure 8.
The results produce a quadratic equation seen in Equation 14 with a perfect correlation coefficient of 1.
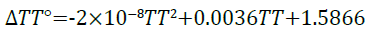 (14)
(14)
The quadratic nature of the fitted model data can be attributed to the dependence of entropy on temperature as a result of the variation of heat capacitance change with temperature according to;
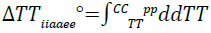 (15)
(15)
Entropy is a measure of the molecular disorder in a system [27]. Greater entropy means a higher disorder in the system. The input of heat and work (energy) across a system boundary alters the entropy of the system such that the greater the amount of energy applied, the greater the rise in entropy.
Results presented in Figure 8 show the lowest value of entropy at the lower bounds of 298K (25°C) which suggests that it is at this temperature that the most ordered arrangement of an adsorption layer will be formed. Simple kinetics explains this phenomenon; the input of heat into a system causes an increasing temperature which results in a greater vibrational energy obtained by the molecules, making the formation of a steady, well-formed boundary layer more difficult.
It is known from literature that the effective temperature range of imidazoline is between 290K and 350K (17°C -77°C). Studies done by Hong et al. [28] indicate that when the temperature is above an effective range, the imidazoline ring becomes unstable. Since the ring is attributed to the adsorption, the increase in system entropy will cause greater disorder to the imidazoline ring thus preventing the formation of a well formed protective barrier against corrosion.
Generally, in an adsorption process, the entropy tends to decrease due to the exothermic nature of the reaction [29]. However, when the system is endothermic the entropy is increased. Adsorption under endothermic conditions causes the adsorbate molecules to disassociate into atoms. The movement of these atoms over a large surface coverage results in an increase in the entropy of the system [29].
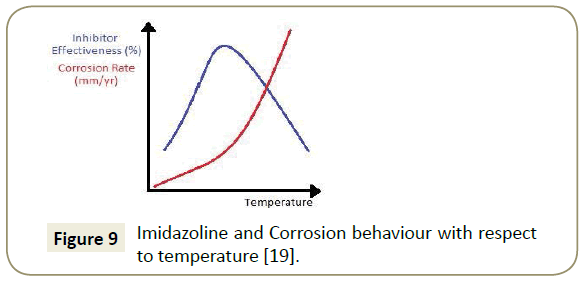
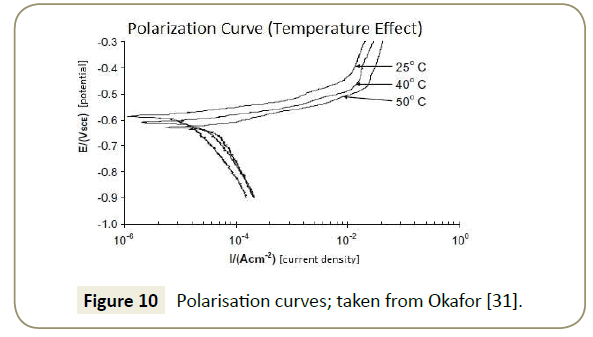
Imidazoline’s corrosion inhibition performance is affected by changing the operating temperature of the pipeline. As is illustrated in Figure 9, the general trend is such that an optimum exists; if the temperature is too low, the molecules lack energy and if the temperature is too high, the formation of an effective layer is compromised. Included in Figure 9 is the general trend of corrosion rate with an increasing temperature; Olivares-Xometl et al. [19] suggests that there is an exponential increase in corrosion rate, through modeling with the Arrhenius Equation. In physical terms, with more energy in the system, the activation energy for the corrosion reactions can be attained more easily. There is also a higher activity of carbon dioxide molecules with this additional energy and this favours the formation of hydrogen ions which more rapidly react with water to form corrosion [30]. Polarisation curves generated by Okafor et al. [31] illustrated that the cathodic corrosion reaction increases under raised temperature, thereby confirming the Arrhenius modelling, see Figure 10.
As the temperature of the system reaches the higher end of the plot, there is drop in effectiveness due to the lack of adsorption of imidazoline molecules. Many different studies have been carried out in this area and have suggested a variety of reasons for this trend. Zhung [18] completed Electrochemical Impedance Spectrum (EIS) analysis which illustrated that with higher temperatures the pipe wall interface capacity increases due to favourable desorption of imidazoline. The decrease in surface coverage has also been attributed to excessive molecular energy which leads to desorption and vibrational detachment [19]. Olivares-Xometl et al. [19] has included results which imply that at higher temperatures, Imidazoline molecules prefer to form the bilayer, rather than actually adsorbing to the pipe wall; this is attributed to the thermodynamic favourability and low energy pathway [32].
Jovancicevic et al. [14] suggests in his research that Imidazoline molecules will also hydrolyse and form their amide precursor under high temperature conditions. The Imidazoline ring is also thought to become increasingly unstable with a temperature rise [28]. Both these suggestions imply that there will be a decreasing amount of Imidazoline available for adsorption. On the low temperature end of the plot, the drop-in effectiveness is due to the lack of energy for Imidazoline adsorption. These temperatures also lead the moisture in the system to form condensates more rapidly and block imidazoline access to the pipe wall [20].
Predictions for the optimum performance temperature have been provided in the Imidazoline research by Ramachandran. The study illustrated the stability of the alkyl chains of ten to twenty carbon atoms in moderate temperatures and for this range it was suggested that the best effectiveness is achieved in a range of 296 K to 350 K.
Due to the increase in entropy with increasing temperature, the imidazoline molecule vibration is greater thereby making it more difficult for the ring to form a steady, well-formed barrier. To ensure that imidazoline performs optimally, other thermodynamic aspects such as Gibbs free energy and enthalpy must be analysed in accordance with entropy.
Impact of temperature on thermodynamic properties
Through the evaluation of the temperature dependent phonon from the simulation results, the impact of temperature on thermodynamic properties can be analysed to determine the effect of temperature on corrosion inhibition. The thermodynamic properties that affect the corrosion inhibition performance of imidazoline include Gibbs free energy and enthalpy.
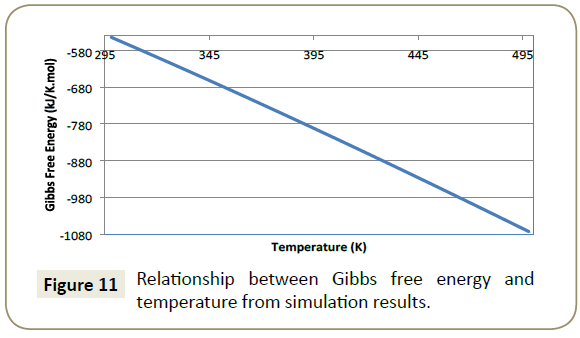
Gibbs free energy: Figure 11 illustrates that as temperature of the system increases, a more negative the value of Gibbs free energy was obtained. The results produce a quadratic relationship between Gibbs free energy and temperature;
A perfect quadratic regression of 1 for the relationship show in Equation 16, clearly suggests that Gibbs free energy increases as the temperature of the system increases.
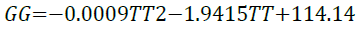 (16)
(16)
A spontaneous process is one in which a negative Gibbs free energy value is produced (Smith, 2005). It is evident from the simulation that the adsorption of imidazoline onto a metal surface is in fact a spontaneous process and the adsorption of imidazoline becomes more spontaneous as temperature increases. However, if higher temperatures were to be used the entropy of the system (S) would increase. The ordered arrangement of imidazoline would be compromised which would result in difficulty in forming a steady well-formed barrier.
Gibbs free energy is calculated by Equation 17.
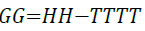 (17)
(17)
Gibbs free energy is also able to predict the type of adsorption that is occurring. For chemisorption to occur Gibbs free energy must be more negative than -40 kJ/mol [33]. Within the effective temperature range (17°C to 60°C), Gibbs free energy results indicate that chemisorption is occurring.
Beyond the effective temperature range of imidazoline, chemisorption will continue to occur more spontaneously. However, due to the simultaneous increase in entropy, there will be a greater molecular disorder in the system which compromises the quality of the protective barrier formed by imidazoline ring. This is affirmed by the Electrochemical Impedance System study conducted by Zhung et al. [15] where an increase in the desorption rate of imidazoline resulted as the pipeline temperature increased.
Enthalpy: Enthalpy is a measure of the total heat content of a system. Enthalpy is calculated from Equation 18.
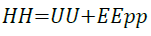 (18)
(18)
The simulation results obtained for internal energy and entalphy for imidazoline are very similar. This is explained as the pressure and volume of the system are kept constant at 101.3 kPa and 9461.2 × 1010 Å3 respectively. The value of PV is calculated by the following equation:
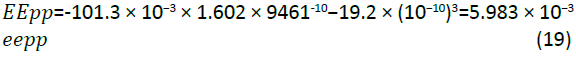
Due to the small and constant value of PV, the enthalpy values present very similar results to the internal energy.
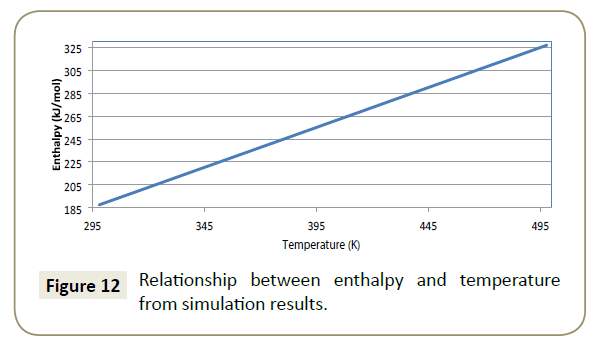
Figure 12 presents the modelled relationship between enthalpy and temperature.
A linear regression of 1 for the relationship between enthalpy and temperature given by Equation 20 presents a perfect model data fit.
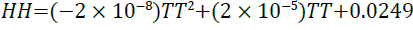 (20)
(20)
Positive values of the simulation results indicate that when chemical bonds are formed between adsorbate and adsorbent, energy is absorbed rather than released into the environment. A chemisorption process has an enthalpy value around 200 kJ/mol (Verma, Khanna and Kapila). Within the effective temperature range of imidazoline (17°C - 60°C), the enthalpy values were between 187 kJ/mol and 221 kJ/mol, suggesting that the adsorption of imidazoline is an endothermic chemisorption process.
As stated by Liu et al. [7] and Edwards et al. [16], a metal surface that has water bounded to it will influence the adsorption of the imidazoline ring by both restricting the available surface area for adsorption to occur and breaking down the N=C double bond of the imidazoline molecule. Energy in excess of 167.5 kJ/mol must be obtained in order to displace the water. If the water is not displaced there will be limited space which allows only one nitrogen atom to adsorb. This increases the angle at which the alkyl chain settles [20]. The alkyl chain tilt identifies that the effective alkyl chain angle is 66°-71° to the normal, however this increases to approximately 40° normal in the presence of water [20].
Due to the presence of water and catalytic basic ions, a ringopening hydrolysis reaction will breakdown the N=C double bond which will result in a de-cyclised imidazoline compound. This decyclised form of imidazoline will not adsorb to the metal surface with the same strength as the ring due to the lower electron donating capability of the imidazoline head. In order to displace the water, the energy required is 44 kcal/mol, which is equivalent to 167.472 kJ/mol. The simulation enthalpy results verify that more than the required energy to displace the water molecules was provided, thus nullifying the affect this phenomenon would have on the adsorption of imidazoline within this temperature range.
The endothermic nature of the process casuses the imidazoline molecules disassociate into atoms when adsorption takes places.
As a result, atomic bonding occurs between the imidazoline and pipeline [29]. This atomic bonding is a result of the transfer of valence electrons from the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) of both the imidazoline and the steel pipeline. According to Zhung [18] the atomic bonding that leads to the creation of the adsorption layer is between the N=C-N region of the imidazoline ring and the iron atoms in the pipelines. As the enthalpy is enough to displace the water, the imidazoline head group is able to from a coordinate covalent bond through the HOMO and LUMO mechanism thus becoming an effective adsorbent for corrosion inhibition.
Impact of temperature on the material’s efficiency
This study has shown that temperature variation impacts the operating conditions by affecting the Helmholtz free energy, enthalpy, entropy, Gibbs free energy and heat capacity. It is feasible that these thermodynamic properties may have extended impacts on the functional ability of the material itself by affecting its properties. These impacts include imidazloine solubility and permeability of the imidazoline layer. Further, during operation, temperature variation affects the velocity of the pipeline contents which impacts upon the inhibition efficiency of imidazoline.
Effect of temperature on imidazoline solubility: From the Second Law of Thermodynamics states that no system exists where heat can be converted solely into work [26]. This suggests that heating a solution enables the particles to move more freely between the solution and the gas phase. The Law predicts that movement will be to the more highly dispersed, disordered state; hence the gas phase, reducing solubility. This establishes that there exists a relationship between temperature and solubility.
The solubility of imiazoline varies from fairly soluble to highly dispersible, influencing the rate at which the inhibitor molecules are transported to the pipe wall [14]. Low solubility in the water phase is positive because this implies that the imidazoline will provide a strong hydrophobic layer [30]; however, there is a simultaneous reduction in the rate in formation of this layer due to the inability to disperse through the water stream. The hydrophilic head group (imidazoline ring) is critical to the solubility of the molecule, as discussed in Chapter 2. In an aqueous medium, adsorption of imidazoline to the metal wall is preferential. This can be affiliated to the larger adsorption energy possessed by the inhibitor molecule compared to the water molecule [18]. Although longer alkyl chains decrease the solubility of imidazoline in water [20], it also increases the adsorption energy, which strengthens the interaction between the metal surface and the inhibitor. A metal surface which is more polar in nature will promote greater adsorption energy than a non-polar surface [18]. This solubility property is important when water flow in the natural gas stream is dispersible, such as bubble flow, caused by similar gas and liquid velocities [34].
As the water in the system tends to follow uniform flow patterns, such as stratified or annular flow, there is a layer of water along the pipe wall [34]. In this case, water soluble imidazoline molecules will result in high corrosion inhibition efficiency. These molecules will diffuse through the water barrier more easily and therefore have greater tendency to adsorb to the metal surface.
It has been suggested that converting imidazoline to a salt will improve its solubility. The use of a carboxylic acid pendant chain will result in the formation of an imidazoline salt with high solubility [30]. There is, however, a tendency for the imidazoline ring to hydrolyse in the presence of water and a basic catalyst. The longer the imidazoline is free in water, hydrolyses rates will be greater and there will be a reduction in the available number of effective molecules. Water is typically the vehicle of imidazoline injection to a natural gas stream. However, imidazoline shows excellent solubility in aliphatic solvents and this property could be exploited as an alternative method of pipeline injection. Imidazoline compounds also exhibit good solubility in oil streams [6], which makes them an ideal candidate as a corrosion inhibitor upstream at the natural gas/oil well.
Effect of temperature on natural gas velocity: The relationship between the gas velocity and temperature is proportional, hence when the temperature of gas is increased, the velocity of the gas increases as well. This is due to the fact that the greater the temperature of the gas, the higher the kinetic energy will be in the gas molecules. Just like how there is an optimal temperature range for the inhibition of imidazoline, there is also an optimal range for the gas velocity in the pipeline.
If the gas velocity travels too slow the diffusion rate of imidazoline will be low [14]. This means that the injected imidazoline is unable to work as efficiently as possible to form the protective layer. As the gas velocity increases, so too will the rate of imidazoline diffusion in the pipeline to from the protective layer.
However, eventually the increase in gas velocity will decrease the effectiveness of the protective imidazoline layer. In temperature terms this is due to the increase of entropy but in terms of gas velocity, continual increases will cause the Reynolds number to increase. The Reynolds number, Re, is defined by the following equation;
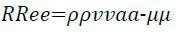 (21)
(21)
When the Reynolds number increases due to the increase in gas velocity, the gas flow in the pipeline becomes turbulent. Turbulent flow causes instability in the pipeline, which causes the formed protective layers of imidazoline to be removed due to the excessive shear stress that is applied [13]. It has been suggested that optimal imidazoline performance occurs at a pipeline velocity in the range of 3 m/s to 35 m/s.
Impact on flow regime: The flow regime in a gas pipeline is essential to the imidazoline inhibitor effectiveness. Flow regimes are influenced by the velocity of the natural gas which is directly related to temperature. For various flow regimes the position of the liquid phase along the pipe’s cross-section is directly related to the effectiveness against corrosion inhibition.
Annular flow: Annular flow occurs when the gas velocity is much greater than that of the liquid. The liquid in this case tends to flow along the pipe wall forming a stable layer of imidazoline [34]. This is due to the fact that the layer of liquid sufficiently covers the wall of the pipeline and when the water soluble imidazoline is injected, it is able to form the protection layer on the pipeline wall. Annular flow the pipeline should be at moderate to high temperatures to ensure a high gas velocity and to improve the solubility of imidazoline when it is injected to ensure the formation of the most inhibitive protective layer.
Slug flow: Slug flow occurs when the liquid stream in the pipeline has a high velocity while the velocity of the natural gas is low [34]. This causes a surge in the liquid that causes it to flow like waves. As a result of the liquid surge, the absorbed imidazoline molecules will be disturbed and inhibit imidazoline from forming a consistent strong layer [20]. Low gas velocity result in low diffusion rates, attributed to the liquid surges caused by slug flow that disturb the formation of a strong and consistent imidazoline protective layer. Lower pipeline temperatures cause a decrease in gas velocity and cause slug flow, effectively inhibiting the stability of the imidazoline layer.
Impact of temperature beyond effective range
This study supports current literature that the effective temperature range for corrosion inhibition of imidazoline is approximately 17 to 60°C. Beyond this range, the conditions support the mechanisms of corrosion, which cause detrimental effects to the integrity of the pipe wall.
Due to the ability of the initial products to undergo subsequent reduction, sweet corrosion is one of the most detrimental forms of corrosion, as the following sweet corrosion reactions will illustrate [15]. The carbon dioxide molecules will react with any moisture in the system to produce corrosive carbonic acid [31]. The equilibrium reaction occurs in the following mechanism;
CO2+H2O↔H2CO3
where H2CO3 in solution will form H+ and CO32- ions (Liu).
ANODE: Fe(s) ↔ Fe2+(aq) + 2e-
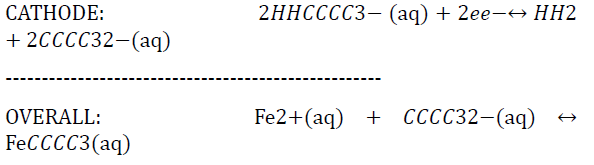
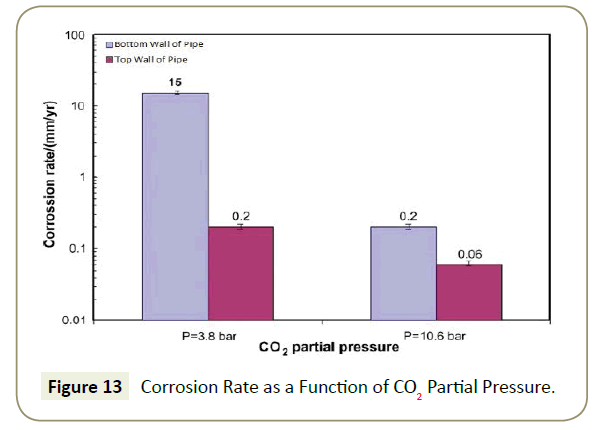
The Fe2+ ions are then able to react with the CO32- generated from the dissolution of carbonic acid to form FeCO3 scale along the wall as a result of the super saturation of the iron and carbonate ions. This scale film does actually prevent further corrosion [13] along the steel surface by acting as a diffusion barrier to the corrosive species. The effectiveness of this scale depends on the nature in which it was formed. Factors that affect the effectiveness of this scale are temperature, partial pressure of carbon dioxide and flow conditions. If the CO2 concentration is at excessive levels, this scale will precipitate out fast enough to form a protective layer, before deeper corrosion can initiate as Figure 13 illustrates.
Conclusion
This study has confirmed the ability of imidazoline as an effective corrosion inhibitor in natural gas pipelines, within an optimal temperature range, through the thorough investigation of thermodynamic data at different temperatures to evaluate its adsorption capabilities. It also showed that the adsorption process occurs spontaneously through a chemisorption mechanism, probably due to its structural distribution and functional groups. As the operating temperature increases, the molecules gain enough kinetic energy to displace the water bound to the metal surface which allows stronger adsorption of the imidazoline ring to the metal surface thus forming a better inhibitive barrier. However, this increase in kinetic energy is also linked to an increase in the disorder of the system, hindering the formation of a steady, uniform boundary layer. Hence, an optimal temperature range exists. This study confirms literature [15,19,34] which suggests that an optimal range exists between 298K and 333K. A cooler temperature will result in the inability to displace the bound water molecules which will break the N=C double bond and cause a decyclised compound, but a higher temperature will cause greater disorder and the associated increase in kinetic energy will aid in the destruction of the boundary layer.
This study has verified the effectiveness of imidazoline as a corrosion inhibitor for its application in natural gas pipelines within the temperature range of 298K to 333K. Many factors affect the performance of imidazoline however, and further work must be done to establish the optimal conditions and molecular structure to comprehensively understand the molecular mechanics of imidazoline and ultimately, its corrosive inhibition potential.
References
- Hopkins P (2014) Assessing the Significance of corrosion in onshore oil and gas pipelines. Underground Pipeline Corrosion. ME Orazem, Woodhead Publishing, pp: 62-84.
- Jaal RA, Ismail MC, Ariwahjoedi B (2014) A Review of CO2 Corrosion Inhibition by Imidazoline-based Inhibitor. MATEC Web of Conferences 13: 05012.
- Likhanova NV, Domínguez-Aguilar MA, Olivares-Xometl O, Nava-Entzana N, Arce E, et al. (2010) The Effect of Ionic Liquids with Imidazolium and Pyridinium Cations on the Corrosion Inhibition of Mild Steel in Acidic Environment. Corrosion Science 52: 2088-2097.
- Rostami A (2009) Review and Evaluation of Corrosion Inhibitors Used in Well Stimulation. Society of Petroleum Engineers, Texas A&M University.
- Obot IB, Macdonald DD, Gasem ZM (2015) Density functional theory (DFT) as a powerful tool for designing new organic corrosion inhibitors. Part 1: An overview. Corrosion Science 99: 1-30.
- Tang S, Jiang Z, Mao Q (1994) New Inhibitor Reduces Corrosion in Crude Tower Overhead. Oil and Gas Journal 92: 68-70.
- Liu J, Yu W, Zhang J, Hu S, You L, et al. (2010) Molecular Modelling Study on Inhibition Performance of Imidazolines for Mild Steel in CO2 Corrosion. Applied Surface Science 256: 4729-4733.
- Zhang K, Xu B, Yang W, Yin X, Liu Y, et al. (2015) Halogen-substituted imidazoline derivatives as corrosion inhibitors for mild steel in hydrochloric acid solution. Corrosion Science 90: 284-295.
- Xia S, Qiu M, Yu L, Liu F, Zhao H (2008) Molecular Dynamics and Density Functional Theory Study on Relationship Between Structure of Imidazoline Derivatives and Inhibition Performance. Corrosion Science 50: 2021-2029.
- Aljourani J, Raeissi K, Golozar MA (2009) Benzimidazole and its Derivatives as Corrosion Inhibitors for Mild Steel in 1M HCl Solution. Corrosion Science 51: 1836-1843.
- Mazumder MA, Al-Muallem HA, Ali SA (2015) The effects of N-pendants and electron-rich amidine motifs in 2-(palkoxyphenyl)-2-imidazolines on mild steel corrosion in CO2-saturated 0.5 M NaCl. Corrosion Science 90: 54-68.
- Du L, Zhao H, Hu H, Zhang X, Ji L, et al. (2014) Quantum chemical and molecular dynamics studies of imidazoline derivatives as corrosion inhibitor and quantitative structure-activity relationship (QSAR) analysis using the support vector machine (SVM) method. Journal of Theoretical and Computational Chemistry. 13: 1450012.
- Tan YJ, Bailey S, Kinsella B (1996) An Investigation of the Formation and Destruction of Corrosion Inhibitor Films using Electrochemical Impedance Spectroscopy (EIS). Corrosion Science 39: 1545-1561.
- Jovancicevic V, Ramachandran S, Prince P (1999) Inhibition of Carbon Dioxide Corrosion od Mild Steel by Imidazolines and Their Precursors. Corrosion 55: 449-455.
- Zhang X, Wang F, He Y, Du Y (2001) Study of the Inhibition Mechanism of Imidazoline amide on CO2 Corrosion of Armco Iron. Corrosion Science 43: 1417-1431.
- Edwards A, Osborne C, Webster S, Klenerman D, Joseph M (1994) Mechanistic Studies of the Corrosion Inhibitor Oleic Imidazoline. Corrosion Science 36:315325.
- Cruz J, MartínezÃÆâÃâââ¬ÃâÃÂAguilera LM, Salcedo R, Castro M (2001) Reactivity Properties of Derivatives of 2Imidazoline: An ab initio DFT Study. International Journal of Quantum Chemistry 85:546-556.
- Zhang J, Qiao G, Hu S, Yan Y, Ren Z, et al. (2010) Theoretical Evaluation of Corrosion Inhibition Performance of Imidazoline Compounds with Different Hydrophilic Groups. Corrosion Science 53: 147-152.
- OlivaresÃÆâÃâââ¬ÃâÃÂXometl O, Likhanova NV, MartínezÃÆâÃâââ¬ÃâÃÂPalou R, DomínguezÃÆâÃâââ¬ÃâÃÂAguilar MA (2009) Electrochemistry and XPS Study of a Imidazoline as Corrosion Inhibitor of Mild Steel in Acidic Environment. Materials and Corrosion 60: 14-21.
- Ramachandran S, Jovancicevic V (1999) Molecular Modelling of the Inhibition of Mild Steel Carbon Dioxide Corrosion by Imidazoline. Corrosion 55: 259-267.
- Akindeju MK, Pareek VK, Rohl AL, Carter DJ, Tade MO (2010) Constant Pressure Mollecular Modelling of Six Optimised Titanium Oxide Polymorphs: Metal Oxide Semiconductors. International Journal of Chemistry 2: 26-37.
- Gale JD (2005) GULP: Capabilities and prospects. Zeitschrift für Kristallographie-Crystalline Materials 220: 552-554.
- Doitpoms.ac.uk (2004) Doitpoms-TLP Library Crystallography-Lattice Geometry.
- Carpy A, Atfani M, Stähle H (1987) Crystal and molecular structure of 2-[N-allyl-N-(2,6-dichlorophenyl)amino]-2-imidazoline hydrobromide. Arch Pharm (Weinheim) 320: 515-519.
- Massa W (2004) Crystal Structure Determination. Berlin: Springer.
- Smith JM, Van Ness HC, Abbott NM (2005) Introduction to Chemical Engineering Thermodynamics. McGraw Hill, New York, USA.
- Dincer I, Cengel YA (2001) Energy, Entropy and Exergy Concepts and Their Roles In Thermal Engineering. Entropy 3: 116-149.
- Hong T, Jepson WP (2001) Corrosion Inhibitor Studies in Large Flow Loop at High Temperature and High Pressure. Corrosion Science 43: 1839-1849.
- Verma NK, Khanna SK, Kapila B (2008) Comprehensive Chemistry: V. XII. New Delhi: Laxmi Publications.
- Gusmano G, Labella P, Montesperelli G, Privitera A, Tassinari S (2006) Study of the Inhibitor Mechanism of Imidazolines by Electrochemical Impedance Spectroscopy. Corrosion 62: 576583.
- Okafor PC, Liu X, Zheng YG (2009) Corrosion Inhibition of Mild Steel by Ethylamino Imidazoline Derivative in CO2 Saturated Solution. Corrosion Science 51: 761-768.
- Lopez DA, Simison SN, De Sanchez SR (2005) Inhibitors Performance in CO2 Corrosion EIS Studies on the Interaction Between their Molecular Structure and Steel Microstructure. Corrosion Science 47: 735-755.
- Fuchs-Godec R (2006) The Adsorption, CMC Determination and Corrosion Inhibition of Some N-Alkyl Quaternary Ammonium Salts on Carbon Steel Surface In 2M H2SO4. Colloids and Surfaces A: Physicochemical and Engineering Aspects 280: 130-139.
- Rafiquee MZ, Khan S, Saxena N, Quraishi MA (2009) Investigation of some Olechemicals as Green Inhibitors on Mild Steel Corrosion in Sulphuric Acid. Journal of Applied Electrochemistry 39: 1409-1417.
Open Access Journals
- Aquaculture & Veterinary Science
- Chemistry & Chemical Sciences
- Clinical Sciences
- Engineering
- General Science
- Genetics & Molecular Biology
- Health Care & Nursing
- Immunology & Microbiology
- Materials Science
- Mathematics & Physics
- Medical Sciences
- Neurology & Psychiatry
- Oncology & Cancer Science
- Pharmaceutical Sciences